Vodič za decibele: dB i dBm u odnosu na dobitak i millivat

Koncept decibela (dB) je razumljivo težak i zbunjujući za nekoga ko ga tek upoznaje. Kombiniranje specifikacija za pojačanje, snagu i napon (i struju, ali ne tako često) koje miješaju dB, dBm, dBW, vata, milivat, napon, milivolti itd., Često zahtijeva pretvaranje unazad i nazad između linearnih vrijednosti i vrijednosti decibela. Ovaj kratki vodič pomoći će vam da razjasnite razliku između rada s decibelima i rada s linearnim vrijednostima.

Logaritme (zapisnike) prvo je zamislio škotski matematičar John Napier, 1600, kao alat za pojednostavljenje operacija množenja i dijeljenja pretvarajući ih u brže i manje operacije dodavanja i oduzimanja sklonih pogreškama. To je moguće zbog načina množenja dva broja izraženih kao slični osnovni brojevi s eksponentima može se postići jednostavnim sabiranjem eksponenata. Podjela istih brojeva izvodi se oduzimanjem eksponenata. To je jedan od zakona eksponenata, a izgleda ovako:

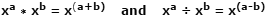
Koristeći stvarne brojeve kao primjer, gdje je x = 10, a = 4, b = 1:

Zakon eksponenata djeluje za bilo koji osnovni broj, a ne samo 10. Da napomenem:

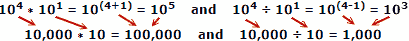
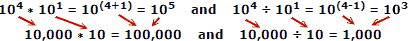
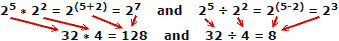
Ljudi imaju tendenciju da prave manje pogrešaka pri dodavanju i oduzimanju brojeva, pa je prednost logaritmija očita. Imajte na umu da su logaritmi razvijeni prije nego što su bila dostupna automatska mehanička ili elektronička računala. Pravilo dijapozitiva koristi svojstva logaritama za proračun, ali to je zasebna glavna tema.

To su jednostavni primjeri, ali vrijede za bilo koju osnovu ili eksponent. U nedostatku kalkulatora, kako biste bili korisni za opću primjenu, potrebna vam je tablica brojeva i njihovi ekvivalentni logaritmi. Tablice ranih dnevnika popunjavali su volumene, ovisno o razmaku između brojeva (1.000, 1.001, 1.002, 1.003, nasuprot 1.0, 1.1, 1.2, 1.3, itd.). Dobra vijest za tvorce tablica logaritma je da je potrebno samo jedno „desetljeće“ brojeva (npr. 1 do 10) jer je svako prethodno ili slijedeće desetljeće jednostavan višestruki broj 10 snage.

Napomena: U ovoj raspravi koristim bazu 10 jer je to osnova našeg zajedničkog brojevnog sustava - otuda i termin 'zajednički logaritam' za osnovne 10 zapisnike. Možda ste čuli za prirodne logaritme, koji koriste bazu e, ali e se ne koristi vrlo često pri izračunavanju skalarne električne snage, napona i struje (iako se koristi kada su uključeni fazni kutovi, tj. Eulerov identitet). Prirodni logaritmi pišu se kao ln (x) bez 'e' podpisa, dok se osnovni 10 logaritmi pišu jednostavno kao log (x) bez 10 podpisa; tj. ne loge (x) ili log10 (x), respektivno.

Po bazi = 10 tablica dnevnika:

Polumaragarmički 5 Cycles Engineering Grafički papir - RF Cafe Izuzetak i poseban slučaj je logx (0) = nedefiniran. To je tako jer nema snage na kojoj možete podići bilo koji broj i dobiti 0 (nulu). Možete asimptotski pristupiti nuli, ali ne možete doći do nule. Nikad se na skali za zapisnik neće prikazati broj nula; obično rade od neke snage 10 do neke druge snage deset. Primjer papira s grafikonima dnevnika prikazan je s desne strane. Sadrži 5 'cikluse' ili 'desetljeće' raspona. Imajte na umu da na osi y nema ništice.

Bazni-10 (uobičajeni) logaritam broja je, dakle, eksponent koji 10 mora podići da bi se dobio taj broj. Drugim riječima, budući da je 10 podignut na snagu 2 jednak 100 (102 = 100), osnovni-10 dnevnik 100 je 2 (log10 100 = 2).

Ovo je osnovni zakon logaritama:


Izvođenje istih množenja i podjela kao i na vrhu stranice pomoću stvarnih logaritama:



To je u redu, ali ono što na kraju završite je logaritam broja koji tražite. Pitanje: Osim jednostavnog primjera poput ovog, kako dobivate odgovor koji vam je potreban? Odgovor: Potražite antilogaritam (antilog) rezultata. U ovom slučaju:

Čvršći i vjerojatniji primjer s brojevima koji nisu cjelobrojne moći 10, mogao bi izgledati ovako:




 HP-35 kalkulator (wikipedia) - RF CafeS obzirom da je logaritam 'x' jednak 1.8444, antilog je 'x', što je 69.9



Računalo sam koristio da bih pregledao zapisnike i antiloge za te brojeve, ali prije 1972-a kada je Hewlett Packard (HP) predstavio svoj znanstveni kalkulator HP-35, prosječna osoba bez pristupa korporativnom ili sveučilišnom mainframe računalu potrebna za upotrebu zapisnika tablice za izvođenje takvih izračuna.

Koga se gnjavi da danas koristim logaritme, pitajte se? Mnogo ljudi, uključujući i mene, često se izračunava kaskadnim parametrima sustava poput slike buke (NF) i presretačkih točaka (IP). Jednostavno zbrajanje i oduzimanje dobitka dB i snage dBm vrijednosti ne djeluju s NF i IP. Formule za upravljanje koriste množenje i podjelu linearnih vrijednosti pojačanja i snage, što zahtijeva prvo pretvaranje dB i / ili dBm u linearne brojeve (omjer pojačanja i mW) pomoću antiloga, izvođenje kaskadnih izračuna, a zatim pretvaranje rezultata natrag u dB i / ili dBm koristeći zapisnike.

Nisu sve kaskade operacija sustava potrebno pretvaranje unazad i nazad. Na primjer, ako je potreban samo ukupni dobitak sustava i / ili razina izlazne snage, izračuni se mogu provesti ili s linearnim jedinicama (mW i množiteljima) ili logaritamskim jedinicama (dBm i dB, respektivno).

Definicije 'dB' i 'dBm'

Decibel (dB) u elektrotehnici je definiran kao 10 više od logaritma baza-10 u omjeru između dvije razine snage; npr. Pout / Pin (dobitak, drugim riječima). Da napomenem:

Svi dobici veći od 1 stoga se izražavaju kao pozitivni decibeli (> 0), a dobici manji od 1 izražavaju se kao negativni decibeli (<0). Imajte na umu da za slučajeve s kojima se većina nas susreće, linearni omjer P1 / P2 mora biti pozitivan broj (> 0) jer je logaritam 0 nedefiniran, a logaritam negativnih brojeva složen (sadrže i stvarni i imaginarni dio ). Vrijednost dB, međutim, teoretski može poprimiti bilo koju vrijednost između −∞ i + ∞, uključujući 0, što je dobitak od 1 [10 * log (1) = 0 dB].

'dBm' je jedinica snage na bazi decibela koja je upućena na 1 mW. Budući da je dobitak 0 dB jednak dobitku od 1, snaga 1 mW je 0 dB veća od 1 mW ili 0 dBm. Slično tome, jedinica snage dBW je decibela u odnosu na 1 W snage.


U skladu s tim, sve vrijednosti dBm veće od 0 veće su od 1 mW, a sve vrijednosti dBm manje od 0 su manje od 1 mW (vidi Sliku 1). Na primjer, + 3.01 dBm je 3.01 dB veći od 1 mW; tj. ili 0 dBm + 3.01 dB = + 3.01 dBm (2 mW). -3.01 dBm je 3.01 dB manji od 1 mW; tj. ili 0 dBm + (−3.01) dB = −3.01 dBm (0.5 mW).

Sljedeća tablica daje nekoliko numeričkih primjera tako da možete vidjeti povezanost između mW i dBm. Isti skup vrijednosti crtanih na logaritamskoj skali proizveo bi pravu liniju. Zbog logaritamskog odnosa, graf spaja manje vrijednosti s lijevom okomitom osi. Uvećana verzija područja 0 do 1 mW umetnuta je radi jasnoće.

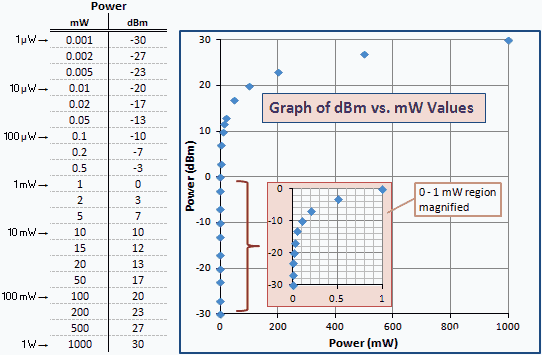
Slika 1 - Grafikon snage u jedinicama dBm vs mW

Sl. 2 je tablica i grafikon omjera dB u odnosu na linearni dobitak sličan dBm u odnosu na mW na Sl. 1. Imajte na umu da su brojevi i krivulje potpuno isti; mijenjaju se samo oznake osi. To je zato što je dBm jedinica snage izražena u dB u odnosu na 1 mW (0 dBm).

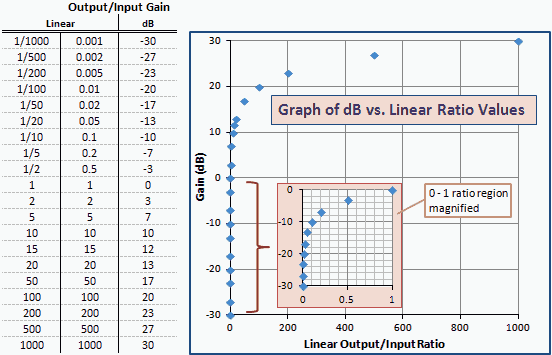
Sl. 2 - Grafički dobitak u jedinicama dBm prema linearnom omjeru

U osnovi, dobitak je faktor množenja (ili podjele). Kao primjer, pojačalo može dobiti pojačanje koje povećava signal za faktor 4 (tj. 4x) od ulaza do izlaza (vidi Sl. 3). Ako se signal 1 mW (0 dBm) dovede u pojačalo, tada izlazi 1 mW * 4 = 4 mW. U smislu decibela, faktor 4 ekvivalentan je zapisu 10 * log (4) = 6.02 dB, tako da 0 dBm plus 6.02 dB dobitka daje + 6.02 dBm na izlazu.

1 mW * 4 = 4 mW

0 dBm + 6.02 dB = 6.02 dBm

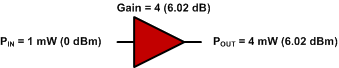
Sl. 3 - Pojedinačno pojačanje pojačala.

Kombinacija dobitaka (linearnih i dB) w / pozitivna vrijednost

Ako je pojačalo s pojačanjem 4 u nizu s drugim pojačalom s pojačanjem 6, tada je ukupni dobitak 4 * 6 = 24. U smislu decibela, faktor 6 je ekvivalentan 10 * log (6) = 7.78 dB, a faktor 24 je ekvivalentan 10 * log (24) = 13.8 dB.

Baš kao što je 4 x 6 = 24 (linearni dobitak), 6.02 dB + 7.78 dB = 13.8 dB (dobitak u decibelima).

Ako se 1 mW signal (0 dBm) dovede u pojačalo, tada 4 mW izlazi iz prvog pojačala, a 24 mW izlazi iz drugog pojačala. Pogledajte Sl. 4.

1 mW * 4 * 6 = 24 mW
0 dBm + 6.02 dB + 7.78 dB = 13.8 dBm

Sl. 4 - Kaskadno pojačanje s dvostrukim pojačalom.

Kombiniranje dobiti i gubitka (linearno i dB)
Sljedeći primjer pokazuje što se događa kada se naiđe na dobitak <1 (gubitak), gdje se prigušivač s pojačanjem 1/6 postavlja nakon prvog pojačala, umjesto da ima drugo pojačalo. Pogledajte sliku 5.
4 * 1 / 6 = 2 / 3 (linearni dobitak). Slično tome, 6.02 dB - 7.78 dB = −1.76 dB (pojačanje u decibelima).
Kao i u prethodnom primjeru, ako se 1 mW signal (0 dBm) dovede u pojačalo s pojačanjem 4, tada izlazi 4 mW. Taj 4 mW tada ulazi u atenuator s linearnim pojačanjem 1 / 6 i izlazi na razini snage 4 / 6 mW (2 / 3 mW).
Ukupni dobitak u ovom slučaju je 4 / 6 = 2 / 3, tako da će izlazna snaga zapravo biti manja od ulazne snage.

1 mW * 4 * 1 / 6 = 2 / 3 mW = 0.67 mW

0 dBm + 6.02 dB + (-7.78 dB) = −1.76 dBm

Sl. 5 - Kaskadno pojačanje i prigušivač.

12 mW + 34 mW + 8 mW + 20 dB

Dodatne informacije o logaritmima
Logaritmi proizvoda
Svojstvo logaritama koji se prethodno podrazumijeva implicitno navodi sljedeće i osnova je za dodavanje i oduzimanje vrijednosti logaritama umjesto množenja njihovih linearnih ekvivalenata.

'h * j / k * m / n' može predstavljati kaskadu komponenata koje imaju po tri uređaja (h, j i m) s pojačanjem> 1 i dva uređaja (k i n) svaki s dobitkom <1 (vidi Slika 6). Ukupni dobitak sustava može se izračunati množenjem svih vrijednosti linearnog pojačanja ili zbrajanjem svih vrijednosti pojačanja decibela.

Sl. 6 - Kaskadne komponente

Logaritmi eksponenata
Sljedeće je važno za razumijevanje zašto je dobitak snage u pogledu snage 10 * log (Pout / Pin) dB, dok je napon u pogledu napona 20 * log (Vout / Vin) dB.


što je tako jer je cf jednak c pomnožen sa sobom 'f' puta. Na primjer, ako je f = 4:


Porast snage na temelju snage vs Pojačanja snage na temelju napona
Porast snage je Pout / Pin, a napon je Vout / Vin. Porast snage na temelju omjera snage u decibelima definiran je kao 10 * log (Pout / Pin). Porast snage u odnosu na napon je [(Vout2 / R) / (Vin2 / R)], pošto je po Ohmovom zakonu P = V2 / R. 'R' u nazivnicima otkazuje napuštanje Vout2 / Vin2, što je jednako (Vout / Vin) 2, kako je definirano pravilom eksponenata koji kaže ac / bc = (a / b) c. Stoga:

Važna napomena: Pojačanje napona u smislu napona je 10 * log (Vout / Vin) dB, isto kao i dobitak snage u pogledu snage. Jednadžba primjene jednadžbe 20 * log (Vout / Vin) dB primjenjuje se u naponu tek kada je napon izražen u naponu. To je uobičajena zbrka.


Nijedna operacija u matematici nije proizvoljna, a to vrijedi i zbog toga zašto se gubitak snage signala (dobitak <1) prikazuje kao negativna vrijednost i stoga se oduzima tijekom kaskadnog izračuna. To je jednostavna demonstracija, ali vrijedna spomena.

log (1 / f) = log (1) - dnevnik (f) = 0 - log (f) = -log (f)

Ako želite izgraditi radio stanicu, pojačajte svoj FM radio odašiljač ili vam treba bilo koji drugi FM oprema, slobodno nas kontaktirajte: [e-pošta zaštićena].

Ostavite poruku 

Lista Poruka